Уважаемые читатели!
По мнению автора, наш МИР доверху наполнен волновыми процессами и явлениями. Об этом говорилось много и многими. Это касалось преимущественно нашего осязаемого и наблюдаемого мира. XX век приоткрыл человечеству доступ в микромир элементарных частиц, атомных ядер и их осколков, а также в среду электромагнитного излучения.
Погружение в этот мир с проявлением некоторых закономерностей неизбежно приводит к появлению определенных гипотез, некоторые из которых становятся постулатами, помогающими объяснять то или иное явление. Причем некоторые постулаты не лишены обыденности нашего привычного мира. Например, закрыв от глаз наблюдателя яркое пятно Солнца, мы будем видеть темную сторону предмета, закрывшего Солнце. И мы можем смело и уверенно констатировать, что предмет, закрывший Солнце мог либо поглотить солнечные лучи, либо их отразить.
В спектрографии наблюдаются аналогичные явления для определенных частот излучения (линии поглощения).
В предлагаемой статье автор, в частности, используя математический аппарат, применяемый для описания Эффекта Доплера и наделив движущийся объект собственным колебанием попытался показать, что излучение, аналогичное белому шуму (солнечный свет) вызывает в отраженном излучении от движущегося объекта «линию поглощения» на частоте собственного колебания объекта. В статье объяснены и другие примеры.
Радикальность данной статьи нивелируется ее статусом – гипотеза.
Приятного чтения.
https://sci-article.ru/stat.php?i=1454335538
Статья опубликована в научном журнале «SCI-ARTICLE.RU» №30 (февраль) 2016
2024-10-06
Утешев Игорь Петрович
Аннотация:
В этой статье описывается механизм концентрации волновой энергии при взаимодействии специальным образом структурированного периодического волнового сигнала и колеблющихся с определённой частотой частиц или объектов, далее называемых осцилляторами. На основе изложенного в статье механизма концентрации волновой энергии сделана попытка объяснить такие природные явления как светящиеся в атмосфере шары, свечение фотосферы Солнца и некоторые другие природные явления.
Abstract:
This article describes the mechanism of concentration of wave energy in the interaction in a special way structured periodic wave signal oscillating with a certain frequency of particles or objects, hereinafter referred to as oscillators. On the basis set out in article mechanism of concentration of wave energy made an attempt to explain natural phenomena such as glowing orbs in the atmosphere, the illumination of the Solar photosphere and some other natural phenomena.
Ключевые слова:
Волновая энергия; волновой сигнал; отраженный сигнал; осциллятор; эффект Доплера; периодическое воздействие; спектр частот; фотосфера Солнца; голос моря; сердце; жизнь; Благодатный огонь.
Keywords:
Wave energy, wave signal; the reflected signal; the oscillator; the Doppler effect; the periodic influence; range of frequencies; the photosphere of the Sun; the voice of the sea; heart; life; the Holy fire.
УДК 51; 53; 61
Актуальность статьи заключается в том, что в ней сделана попытка объяснить механизм концентрации волновой энергии, который практически присутствует повсеместно в пространстве.
Введение
В статье описывается взаимодействие волновых процессов с так называемыми осцилляторами – колеблющимися объектами или частицами. Такими объектами насыщено все окружающее пространство. Это могут быть частицы микромира, волны на поверхности жидкости, капли дождя, движение растительности от воздушных потоков, биение сердца, вращающиеся объекты и ещё многое другое.
Среда существования этих частиц или объектов наполнена волнами. Эти волны могут быть акустические, электромагнитные и вероятно ещё какие-то, которые знакомы на слух, но ещё пока неосязаемы.
Для большинства из нас волновой процесс ассоциируется с гармоникой, описываемой через тригонометрическую функцию. В данном случае в статье рассматриваются более сложные структурированные периодические волновые процессы.
Особенности взаимодействия периодических волновых процессов с осцилляторами исследованы на математической модели, которая была получена из соотношений, описывающих эффект Доплера.
Эффект Доплера для колеблющегося объекта (осциллятора)
В радиолокации широко распространён способ определения скорости движущегося объекта, основанный на эффекте Доплера.
В соответствии с данной теорией скорость объекта определяется через частоту сигнала излучаемого источником в сторону объекта - ωиз и частоту отраженного сигнала - ωдоп, регистрируемого приемником. Взаимосвязь этих частот и скорости объекта наблюдения описывается следующими соотношениями:
ωдоп=ωиз/(1-v/u) (объект движется навстречу приемнику);
ωдоп=ωиз/(1+v/u) (объект движется от приемника),
где:
v – скорость объекта;
u – скорость волны.
Если движение объекта является колебательным (в таких случаях объект называют осциллятором), то оба предыдущих соотношения объединяются одним
ωдоп= ωиз /(1-K sin(ωобt)), (1)
где:
K=ΔV/u;
ΔV – амплитуда колебаний объекта по скорости;
ωоб – частота колебания объекта.
В окружающей действительности чаще всего мы сталкиваемся с привычными для нас закономерностями, которые позволяют с высокой достоверностью утверждать, что чем меньше масса объекта, тем значительнее его колебания в окружающей среде смещаются в сторону больших частот и меньших амплитуд.
С учётом того, что скорость используемой волны достаточно велика, то можно утверждать, что коэффициент K в соотношении (1) весьма мал.
В этом случае соотношение (1) с учётом малости коэффициента K можно приближенно записать в следующем виде
ωдоп≈ωиз(1+K sin(ωобt)). (2)
Обоснование этому можно наглядно продемонстрировать на простом примере. Если соотношение (1+Δ) поделить на 1/(1-Δ), где Δ – малая величина, то получим (1-Δ2 ), которое говорит о том, что рассмотренные соотношения отличаются друг от друга на величину, соответствующую второму порядку малости.
Представляя sin(ωобt) через ряд Тейлора, соотношение (2) примет следующий вид:
ωдоп≈ ωиз [1+Kωобt - K(ωобt)3/3!+ …]. (3)
Правая часть соотношения (3) состоит из частоты ωиз и приращения (изменения) частоты излучения.
Перемножив правую и левую части соотношения (3) на t и используя только первый член ряда Тейлора для тригонометрической функции, представим соотношение (3) в несколько ином виде:
Sin(ωдопt) ≈ Sin(ωиз t)[1+KSin(ωобt)-KSin3(ωобt) /3!+ …]. (4)
Таким образом, полученное соотношение (4) можно рассматривать как аналог соотношения (3), который возможно в силу принятых допущений не в состоянии дать достаточно точно количественную оценку, но в данном случае важнее отразить качественный характер изменения отраженного сигнала. Следует отметить, что отраженный сигнал состоит из сигнала излучения и второй компоненты, отражающей приращение (изменение) частоты излучения.
Все эти преобразования были проделаны для того, чтобы описать с качественной точки зрения отраженный сигнал при условии, что сигнал, излучаемый источником в сторону колеблющегося объекта, является периодическим.
Сигнал излучаемого источником в сторону объекта можно разложить в ряд Фурье. Для отдельных гармоник с частотой ωi из, полученного ряда Фурье, будет выполняться соотношение (4).
bi Sin(ωi допt) ≈ bi Sin(ω i из t)[1+KSin(ωобt)-KSin3(ωобt) /3!+ …)], (5)
где bi – коэффициент ряда Фурье i-ой гармоники.
Суммируя соотношения (5) для всех гармоник ряда Фурье получим следующее соотношение:
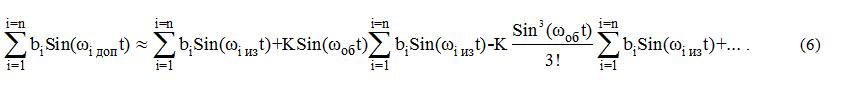
В правой части соотношения (6) первая сумма гармоник является периодическим сигналом излучения в сторону объекта.
Левая часть соотношения (6) является отраженным сигналом, который состоит из излучаемого сигнала и суммы произведений излучаемого сигнала на гармонику в соответствующей степени.
Соотношение (6) фактически является приближенной математической моделью взаимодействия волны и объекта или частицы.
Дополнительные компоненты из соотношения (6), связанные с частотой колебания объекта ωоб, имеют схожий характер изменения частотного распределения, и в частности, на частоте колебания объекта.
Соотношение (6) лучше отражает действительность, если габариты объекта или частицы соизмеримы или превосходят амплитуды гармоник излучаемого источником сигнала.
Колеблющиеся объекты или частицы (осцилляторы), как естественные концентраторы волновой энергии
В качестве сигнала излучаемого источником в сторону объекта можно принять периодическое ступенчатое воздействие Ua(t) , изображенное на рис.1, c частотой периодического сигнала равного 1. А частоту колебания объекта или частицы (осциллятора) считать равной 50. Частота Ua(t) и осциллятора выбраны произвольно.
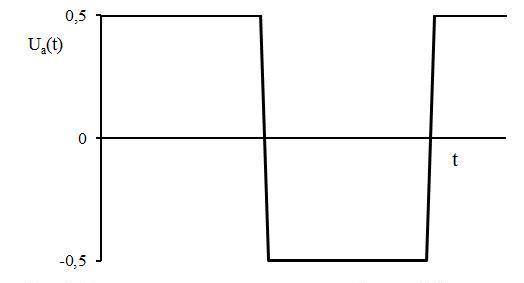
Рис.1. Ступенчатое периодическое воздействие Ua(t).
В этом случае с учётом только первой дополнительной компоненты в (6) получим концентрацию волновой энергии на частоте осциллятора ω=50 рис.2.
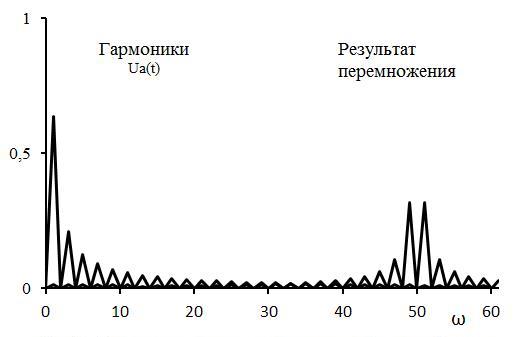
Рис.2. Амплитуды гармоник ступенчатого воздействия Ua(t) и результат перемножения гармоник тригонометрического ряда Фурье, описывающего Ua(t), на гармонику Sin(50t).
На рис.3 изображены гармоники полученного периодического сигнала, амплитуды которого изображены на рис.2. Из рис.3 видно, что вблизи частоты осциллятора образуются две доминирующие разнонаправленные гармоники, в которых концентрируется большая часть волновой энергии.
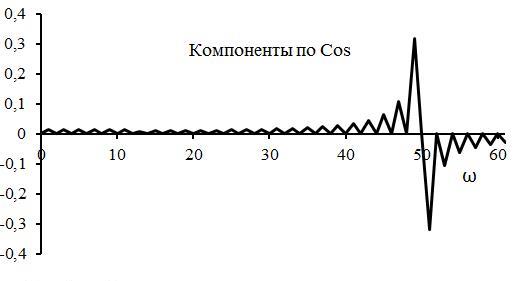
Рис.3 Гармоники, полученные в результате перемножения гармоник тригонометрического ряда Фурье, описывающего Ua(t) на гармонику Sin(50t).
Вполне допускаю, что предложенное ступенчатое воздействие является не единственным, обеспечивающим концентрацию волновой энергии и среди многообразия этих воздействий есть наиболее эффективное.
Если в периодическом воздействии Uа(t) принять амплитуды всех гармоник равными 1 (аналог «белого шума»), то в соответствии с (6), если принять во внимание только первую дополнительную компоненту правой части, получим обнуление амплитуды гармоники на частоте осциллятора ω=50 рис.4.
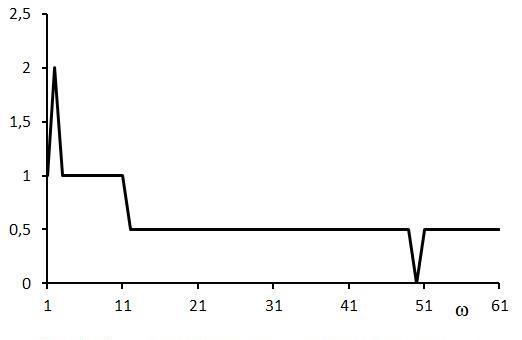
Рис.4. Амплитуды полученных гармоник в результате перемножения периодического тригонометрического ряда (амплитуды гармоник равны 1) с отдельной гармоникой Sin(50t).
Выше сказанное позволяет сформулировать условия, обеспечивающие получения концентрации волновой энергии:
Из рис.2 и рис.4 наглядно видно, что характер спектра отраженного сигнала, с точки зрения возможности концентрации волновой энергии, существенно зависит от спектра сигнала излучаемого источником в сторону объекта. Это, как будет видно из дальнейшего изложения, хорошо коррелируется с условиями, приводящими к появлению темных и ярких линий в спектре раскалённых газов.
Обсуждение некоторых экспериментальных данных
В [1, с.48] описаны эксперименты получения спектральных линий раскалённых солей металлов. Данные эксперименты проводились учёными из Гейдельбергского университета химиком Робертом Бунзеном и физиком Густавом Кирхгофом.
«Они построили стандартный прибор для анализа спектров элементов, входивших в состав солей, которые вносились в пламя (использовалась горелка Бунзена – газовая горелка, в которой сжигалось исследуемое вещество). Они открыли, что яркие линии спектра раскалённых солей металлов являются характерными для определённого металла. Первым практическим доказательством состава вещества было открытие новых элементов: цезия и рубидия. Используя эту экспериментальную методику, Кирхгоф идентифицировал многие тёмные линии Фраунгофера. Например, D-линия принадлежит натрию (рис.10). Давид Брюстер (1781-1868) в 1832г. уже объяснял происхождение тёмных линий солнечного спектра тем, что свет, испускаемый горячей поверхностью Солнца, прежде, чем достигнуть Земли, проходит через внешнюю более холодную атмосферу Солнца, компоненты которой поглощают практически на тех же длинах волн, которые испускаются при более высокой температуре. Таким образом, тёмная линия появляется там, где должна была бы быть яркая линия, если бы не было атмосферы. Например, пары натрия (легко получаемые добавлением в пламя горелки обычной поваренной соли) испускают характерный желтый свет, образуемый двумя узкими и близкими друг к другу линиями. (D-линия). Где бы ни появлялись в спектре эти линии, мы можем с уверенностью утверждать, что в источнике спектра содержится натрий. Это мощнейший метод химического анализа позволяет обнаруживать минимальные следы вещества и не зависит от расстояния до исследуемого объекта, позволяя, например, исследовать звезды.
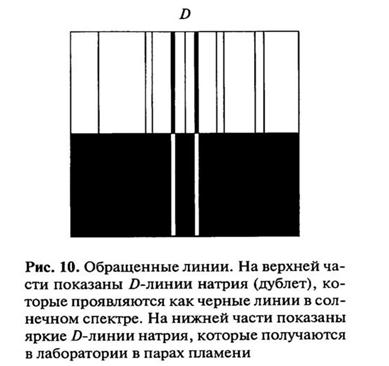
Длины волн излучения, которое испускается веществом, может также и поглощаться на тех длинах волн. Если, например, мы посылаем интенсивный свет, содержащий все видимые длины волн (непрерывный спектр излучения), через пламя в котором сгорает натрий, то в пропущенном свете обнаруживается отсутствие длин волн, соответствующих двум желтым линиям D-линии натрия. В спектре две темные линии появляются в тех местах, в которых наблюдаются две яркие линии в спектре излучения. Это объяснение применимо не только для нашего Солнца, но и для любой звезды. Действительно, темные линии, подобные тем, что Фраунгофер наблюдал в солнечном спектре, наблюдаются и в спектрах звезд, и положение этих линий указывает, какие длины волн поглощаются веществами в звездных атмосферах, что позволяет определить эти вещества».
Из приведенного текста следует:
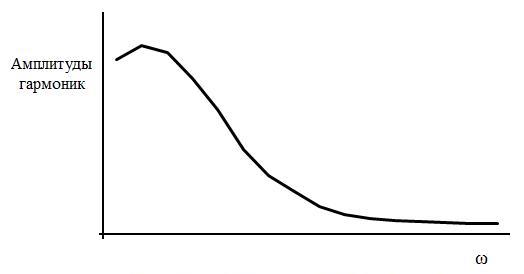
Рис.5. Пример спектра излучения газовой горелки.
На рис.2,4,6,7 отражена только первая дополнительная компонента из правой части соотношения (6). Это сделано только для усиления наглядности. С учётом всех компонент правой части соотношения (6) концентрация волновой энергии на частоте осциллятора при вторичном взаимодействии не исчезает. Более того, концентрация волновой энергии существенно возрастает, в частности, если частота периодического воздействия Uа(t) близка к частоте осциллятора. Наблюдаются признаки резонансного явления. Не исчезает также и относительное уменьшение амплитуды гармоники, которое было показано на рис. 4.
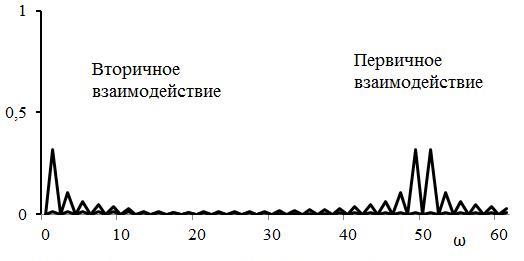
Рис.6. Амплитуды полученных гармоник в результате вторичного взаимодействия с осциллятором, аналогичным при первом взаимодействии.
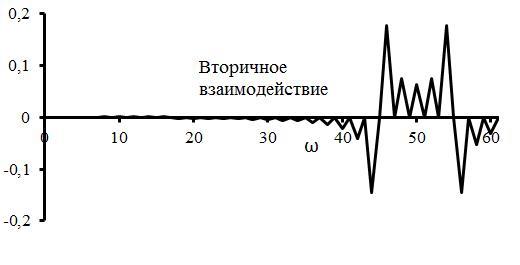
Рис.7. Результат вторичного взаимодействия с осциллятором, описываемым гармоникой Sin(5t).
Необходимо отметить, что приведенные примеры из [1] сравнивались с математической моделью (6) в которой объект или частица являлись осцилляторами с частотами равными частоте излучения или поглощения самой частицей.
Можно провести внешнюю аналогию между рассматриваемым в данной статье отраженным сигналом при периодическом воздействии Ua(t) и спектральными линиями в спектре раскалённых газов. В солнечном спектре, который в определённом диапазоне можно представить как «белый шум», присутствуют черные линии (линии поглощения), которые можно идентифицировать и в рис.4. В рис.2 концентрацию волновой энергии на частоте осциллятора можно идентифицировать как яркие линии в спектре.
Если на осциллятор подавать несимметричный периодический сигнал относительно оси времени, что приводит к появлению константы в описании ряда Фурье, например ступенчатое воздействие рис. 8, то в этом случае наблюдается более значительная концентрация волновой энергии рис.9. При наличии константы в ряде Фурье, описывающего Ua(t) увеличится концентрация волновой энергии и в примерах, изображенных на рис.2,3,6,7.
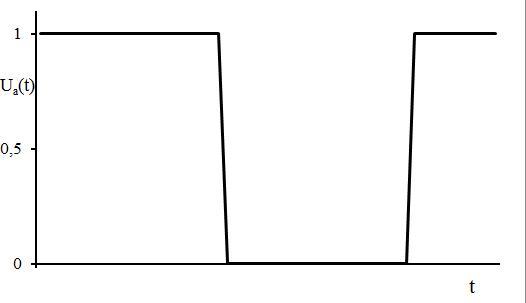
Рис.8. Ступенчатое периодическое воздействие Ua(t).
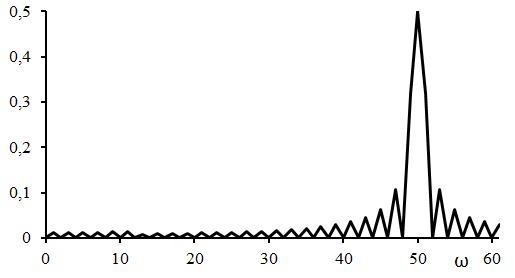
Рис.9 Амплитуды гармоник результата перемножения тригонометрического ряда Фурье, описывающего Ua(t), на гармонику Sin(50t).
В соответствии с современной теорией атом вещества способен самопроизвольно испускать, а также поглощать квант волновой энергии. Величина этой энергии весьма незначительна. Именно поэтому Альберт Эйнштейн отнёсся с некоторыми сомнениями к попытке сгруппировать (объединить) волновую энергию квантов излучения в один электромагнитный поток. Тем не менее, эта идея нашла своё воплощение в лазерах, которые при помощи энергетической накачки атомов используемого вещества способны из отдельных излучений атомов создать единый и весьма значительный электромагнитный поток энергии.
Рассматривая это явление в контексте данной статьи, можно по аналогии с лазером ставить вопрос о возможности объединения множества отраженных сигналов от осцилляторов в единый волновой поток.
Направление суммарного волнового потока для лазера определяют зеркала, поочерёдно отражающие всё более возрастающий поток волновой энергии. Направление же отраженных сигналов от осцилляторов в значительной степени определяется направлением структурированного излучения.
Не являясь профессиональным физиком, могу только предполагать, что концентрация волновой энергии при взаимодействии структурированного периодического волнового сигнала с осциллятором имеет место быть. Очевидно, что любая концентрация энергии в природе приводит к изменению состояния, даже если эта энергия незначительна по величине. При наличии условий суммирования этих малых энергий возможно образование значительных энергетических потоков, которые, как мне представляется, способны стать спусковым механизмом высвобождения энергии заключенной в материи.
Может быть, для наблюдаемого атмосферного эффекта, такого как светящиеся шары в атмосфере вполне достаточно объединение концентраций волновой энергии нескольких осцилляторов, например «пары осцилляторов». Каждый осциллятор из данной пары отражает поочерёдно пришедший сигнал от противоположного осциллятора. На мой взгляд, возможны и более сложные конструкции, такие как «сфера осцилляторов», «цилиндр осцилляторов». Необходимо принять во внимание, что в соответствии с соотношением (6) отраженный сигнал содержит в себе сигнал излучаемый источником в сторону объекта или частицы. Если частота периодического воздействия Uа(t) близка к частоте осциллятора, то этот факт приводит к большему усилению сконцентрированной энергии на каждом этапе взаимодействия отраженного сигнала с осциллятором. В этом случае концентрация волновой энергии существенно повышается. Внешнее волновое воздействие на такую конструкцию можно рассматривать как внешнюю энергетическую подпитку.
Далее будут рассмотрены ещё некоторые физические явления, которые, вероятно, могут быть объяснены с позиции данной гипотезы.
Фотосфера Солнца
Утверждается, что причина высокой температуры фотосферы, а это миллионы градусов в настоящее время не определена.
Если встать на позицию, излагаемую в данной статье, то можно предположить, что Солнце испускает специальным образом структурированный периодический сигнал, который проходя через солнечную атмосферу, концентрирует волновую энергию благодаря взаимодействию с частицами атмосферы. Непрерывное периодическое воздействие со стороны Солнца на окружающую атмосферу приводит:
Если прибавить к этому резонансные явления, которые проявляются когда частота периодического воздействия Uа(t) близка к частоте осциллятора, то это может стать предпосылкой (спусковым механизмом) к высвобождению связанной в частицах материи термоядерной энергии, которая и создаёт высокотемпературную плазму.
Очевидно, что такие процессы возможны при выполнении определённых требований по плотности атмосферы и характеру волнового воздействия со стороны Солнца.
С увеличением высоты над поверхностью Солнца, и уменьшением плотности атмосферы процесс разогрева атмосферы прекращается. Так же процесс разогрева может прекратиться с изменением характера волнового воздействия Солнца.
Появление «темных пятен» на Солнце, вероятно, является именно тем случаем, когда на Солнце локально изменились условия разогрева атмосферы за счет изменения волнового воздействия с поверхности Солнца, которое уменьшает или вовсе прекращает концентрацию волновой энергии. В этих местах атмосфера становится прозрачнее, и волновое солнечное воздействие может беспрепятственно выходить в космическое пространство.
Интересен эффект увеличения свечения «солнечной короны» на границе с «темными пятнами». Если руководствоваться изложенной гипотезой, то можно предположить, что данный эффект вызван тем, что волновое воздействие с поверхности Солнца в местах более яркого свечения фотосферы эффективнее для концентрации волновой энергии, а следовательно и для высвобождения термоядерной энергии.
Увеличение темных пятен на Солнце является признаком увеличения солнечной активности, которая появляется с периодичностью 11 лет. Солнечная активность заметно влияет на климат нашей планеты, на растительный и животный мир. Максимумы солнечной активности также провоцируют развитие многих болезней: в частности, усиливается вероятность эпидемий.
Волновое воздействие непосредственно исходящее из темных пятен на Солнце, достигая атмосферы Земли в состоянии инициировать концентрацию волновой энергии при взаимодействии с осциллятором в атмосфере. Вероятно, эти излучения способствуют образованию, например облаков, которые также можно рассматривать как объекты сконцентрированной энергии. И если это так, то возникает возможность искусственно влиять на изменение структуры атмосферы Земли со всеми вытекающими отсюда последствиями.
«Голос моря»
Уже несколько столетий существует загадка мирового океана, связанная с появлением в море судов без экипажа. Причины этому неизвестны, но высказываются предположения об инфразвуке, вызывающим панику и неадекватные действия экипажа.
В данной статье не случайно многократно повторена фраза о концентрации волновой энергии при взаимодействии с объектом или частицей. Под частицами можно подразумевать атомы и молекулы вещества. Под объектом, например в атмосфере, вполне может быть рассмотрена обыкновенная капля дождя.
Представим, что на море непогода – дождь, сильная облачность с грозой и громом. Высокие волны, порывы ветра создают высокую турбулентность в атмосфере. Снизу море, а сверху затянутое тучами небо.
Это как раз те условия, при которых возможна волновая концентрация энергии. Капли дождя выполняют функции осцилляторов. Гром от молний является излучением акустических волн, которые множатся в пространстве, ограниченном морем и облаками.
Не могу утверждать наверняка, но предпосылки к концентрации акустической энергии имеются. Акустические частоты множатся, так как размеры капель всегда разные и их неустойчивое состояние тоже разное.
В качестве осцилляторов могут выступать и сами морские волны.
Разряды молний создают ступенчатое акустическое воздействие.
Различные по частоте колебания осцилляторы создают условия для появления отраженных сигналов разной частоты. Среди этих частот могут появиться и волновые сигналы с частотой инфразвука.
Данный пример мною приведен скорее для того, чтобы обратить внимание на возможные виды осцилляторов и источников волнового воздействия, обеспечивающих концентрацию акустической волновой энергии и формирования новых акустических частот и, в частности, в области инфразвука.
Медицинский аспект
Все наше пространство, в котором мы живем и которое наблюдаем, пронизывают волны. Считаю, что именно волновая наполненность среды обитания является одним из основных факторов, определяющих состояние нашего организма. Предполагаю, что влияние окружающей среды на живое существо связано с описанным в данной статье эффектом концентрации волновой энергии. От этого нам кажутся отдельные звуки благотворными, а некоторые иные звуки мы воспринимаем как тягостные и некомфортные. Каждый из нас убеждается в этом ежедневно, слушая полюбившиеся мелодии, стихи, просто голоса других людей и многое что другое. Не редко мы связываем это с особой энергетикой того или иного воздействия. Может быть, это определение действительно отражает существо явления. Ведь наш организм во многом насыщен осцилляторами. Наиболее ярким из них является наше сердце. Поэтому не случайно в нашей жизни присутствует такое словосочетание как « я чувствую сердцем …».
Становится распространённым лечебный эффект от общения с некоторыми живыми существами, такими например как дельфины, являющимися источником широчайшего диапазона звуковых сигналов, которые в нашем организме способны концентрировать энергию в нужном месте нашего тела.
Очевидно, что развитие жизни успешно происходит там, где имеются достаточные для этого источники энергии, и если гипотеза о существовании концентрации волновой энергии правдоподобна, то может это и есть энергетическая предпосылка возникновения и поддержания жизни.
Заключение
В данной статье сделана попытка осмыслить возможный механизм концентрации волновой энергии. Для оценки жизненности идеи всегда необходимы расчеты и главное согласие с фундаментальными законами природы. Это важнейший момент и именно поэтому было уделено внимание опытам и устоявшемуся представлению в спектроскопии.
Была использована математическая модель, которая, возможно не без изъянов, даёт качественную оценку механистического взаимодействия структурированного волнового сигнала и осциллятора. Необходимо отметить, что наблюдается некоторая аналогия между характером отраженного сигнала и спектром излучения раскалённых газов. Однако в ряде случаев имеется полная противоположность. В данном случае речь идет о специфичности спектра газовой горелки и влияния его на цвет линий поглощения, а также общепринятого объяснения цвета линий поглощения в спектре солнечного излучения. На мой взгляд, это требует дополнительного осмысления.
В статье высказано предположение, что существуют определенные условия, при которых возможна волновая концентрация энергии при взаимодействии структурированного излучения с осциллятором. Причем, осциллятор никак не связан с какими-либо ограничениями на собственную частоту колебания. В случае совпадений частоты осциллятора с частотой волны, самопроизвольно испускаемой веществом (атомом), возможна полная аналогия внешних проявлений.
В данной статье практически отсутствуют возможные предположения о природе структурированного периодического сигнала. Но если всё сказанное или даже часть от сказанного – ИСТИНА, то природа его всемогуща. Она сродни природе Благодатного огня.
Литература
Рецензии:
3.02.2016, 14:34 Мирмович-Тихомиров Эдуард Григорьевич Рецензия: Статья имеет право на опубликование. Она носит характер сугубо авторского прочтения некоторых нестандартных и известных фактов физики сплошных сред и спектральной диагностики. Рецензент и сам интересуется эффектами встречных треков, обобщением Черенков-эффекта и т.д., которые он "обзывает" "кёрнинг-явлениями", которые, могут восприниматься как индетерминизм распространения волновых пакетов. Рецензентом в своё время были опубликованы факты опережения ионосферными возмущениями геомагнитных бурь и магнитосферных суббурь, перипетиями в зоне каспа при вторжении в него солнечных корпускулярных потоков, ионизирующих нейтральную компоненту полярной атмосферы и др. Возможно, эти воззрения помогут разобраться с выдумками вокруг "красного смещения" спектра водорода и "смешного разбегания" неких фиктивных проективных на наше небо образований, названных галактиками, "на все четыре стороны". Надо подумать. Он много лет посвятил изучению этого смещения спектра в целом. Но рецензент, как всегда, не доволен грамматическими описками и ошибками, некорректностью применяемой арифметики и математики без достаточных объяснений и аргументации (разложение в ряд лишь при малых углах, деление обратных величин для получения второго порядка малости и др.), против яканья в научных статьях, недостаточных ссылок на предшественников (а здесь и вовсе их нет, т.к. фактически неопубликованный материал про лазеры почти не относится к делу). Категорически возражает против безосновательного низвержения циклонального генезиса солнечных пятен и др. Но, ничего из сказанного рецензентом, кроме "пара натрия" и др. грамматики и "падежов", не препятствует публикации, если автор чуть-чуть среагирует на эти строки.
04.02.2016 11:11 Ответ на рецензию автора Утешев Игорь Петрович: Здравствуйте! Благодарен Вам за прочтение и весьма живую реакцию на статью. Хочу особенно подчеркнуть, что не являюсь профессиональным физиком и конечно слаб в области специальной терминологии. Всю свою сознательную (профессиональную) жизнь занимаюсь системами автоматического управления и в большей степени линейными системами. Работая над последней статьей, которая была опубликована в 2015 году в журнале «Радиотехнические тетради», номере №55 обратил внимание на внешнюю похожесть некоторых частотных характеристик линейных систем, имеющих комплексные корни в характеристическом полиноме с частотными спектрами частиц материи. Это подвигло меня более внимательно отнестись к реакции линейных систем на периодическое воздействие. Не буду скрывать, что первоначально обратил внимание на результат перемножения тригонометрического ряда Фурье на гармонику, и только позже у меня появилась ассоциация с взаимодействием частицы и волны. Получив корреляцию результатов перемножения ряда Фурье и гармоники с реальными фактами в спектроскопии, которые изложены в книге о лазере, стал искать математическое подтверждение. Именно поэтому значительная часть статьи посвящена научным результатам в спектроскопии. Что касается замечаний: 1. Обоснованность замены соотношения ωдоп= ωиз /(1-K sin(ωобt)) на соотношение ωдоп≈ ωиз (1+K sin(ωобt)) кажется правомерным, так как коэффициент K=ΔV/u много меньше 1, ввиду того, что скорость распространения волны «u» в среде всегда значительно больше скорости колеблющегося в данной среде объекта «ΔV». В этом случае отношение [ωиз (1+K sin(ωобt))] / [ωиз /(1-K sin(ωобt))] = 1-K2 sin2(ωобt)). Так как величина 1-K2 sin2(ωобt))« 1, то проведенное преобразование вполне корректно для принятых условий; 2. Второе замечание более серьезное. Вы ставите вопрос о правомерности замены соотношения ωдоп≈ ωиз [1+Kωобt - K(ωобt)3/3!+ …] на соотношение Sin(ωдопt) ≈ Sin(ωиз t)[1+KSin(ωобt)-KSin3(ωобt) /3!+ …]. В свою защиту могу сказать следующее: - для малых значений аргумента данные преобразования считаются корректными. Полагаю, что для качественной оценки этот диапазон может составлять не менее ¼ от всего фазового состояния осциллятора. Весь фазовый диапазон осциллятора составляет от 0 до 2π. Это касается также и фазового диапазона сигнала излучаемого источником в сторону объекта; - смягчающим обстоятельством может служить тот факт, что проведенные преобразования были осуществлены одновременно для обеих частей соотношения. В этом случае можно рассчитывать на выполнение условия |Sin(ωдопt)|≤ 1; - получено очень простое и с математической точки зрения красивое соотношение (это мое частное мнение); - именно такое преобразование позволило свести взаимодействие волны и частицы к произведению ряда Фурье и гармоники, а оно, как говорилось выше, коррелирует с результатами спектроскопии; В аргументации присутствует много косвенного и субъективного, но это, наверное, простительно для гипотезы. 3. Что касается "пара натрия" и др. грамматики и "падежов", яканья в научных статьях - признаю безоговорочно. У меня было сомнение в публикации, но однажды наступила гармония. Это произошло после того, как я осознал (интуитивно), что у ПРИРОДЫ очень мало инструментария творить действительность, но те инструменты, которыми ПРИРОДА обладает поистине всемогущи. Поэтому эти инструменты присутствуют везде. И в физике и в теории автоматического управления, которой я отдал много лет жизни. Благодарю Вас за внимательный и доброжелательный отзыв! Здоровья Вам! Утешев И.П.
Комментарии пользователей:
13.02.2016, 0:02 Утешев Игорь Петрович Отзыв: Здравствуйте! Кажется, что всё исправил. Спасибо! Утешев И.П.
Оставить отзыв: